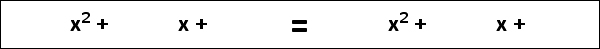Quadratic Formula
Information (Quadratic Expressions, Equations and Functions)
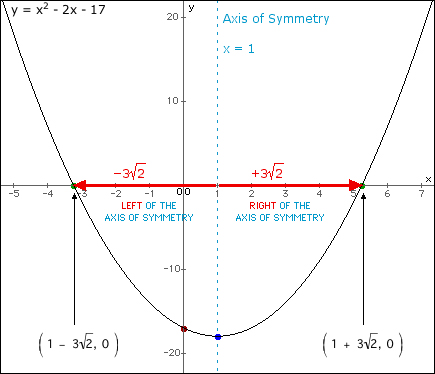
The quadratic formula is one method that can be used to find the roots of quadratic equations of the form ax2 + bx + c = 0.
Click here to see the derivation of the quadratic formula.
The radicand of the quadratic formula (b2 - 4ac) is given the name "discriminant" and is represented by the symbol Δ.
Example
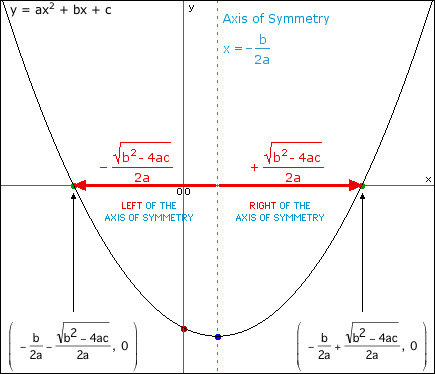
Graphical Interpretation
Consider the graph of the quadratic function y = ax2 + bx + c (and the specific example y = x2 - 2x - 17).
In the case of the specific example y = x2 - 2x - 17, the axis of symmetry is x = 1. The x-intercepts are 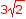 left and right of the axis of symmetry.
left and right of the axis of symmetry.
Demonstration
 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.js

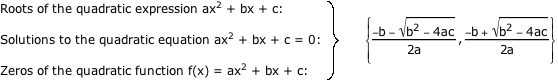






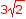 left and right of the axis of symmetry.
left and right of the axis of symmetry.